Halmazok
Halmazok
Először nézzük meg mit is takar maga a fogalom:
Halmaz: elemek összessége (a halmazt magát nemigen szokás definiálni, mivel a matematikában alapfogalomként kezelik).
1. A halmazok megadása
Halmazok megadására többféle módszer létezik, a jegyzetben a következőkkel találkozhat:- elemek felsorolásával (az összes elemet felsorolom, vagy legalább annyit, hogy az alapján következtetni lehessen a többi elemre); például
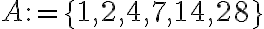 .
.
- a halmaz elemeire jellemző tulajdonság megadásával; pl.: A:={28 pozitív osztói}.
- jellel; pl.:
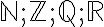
(A jegyzetben 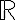 jelöli a valós számok halmazát,
jelöli a valós számok halmazát, 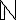 a természetes számok halmazát)
a természetes számok halmazát)
A halmazokat mindig nagybetűvel jelöljük. Az elemeket { } zárójelbe tesszük. Ha egy adott a elem benne van az A halmazban, akkor a következőképpen jelöljük: 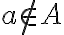 ; ha nincs benne a halmazban:
; ha nincs benne a halmazban: 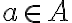 .
.
2. Műveletek
Jelöljük H-val az ún. alaphalmazt legyen adott két tetszőleges halmaz: A és B, amelyek elemei a H halmaz elemei közül kerülnek ki.
Unióképzés (halmazok egyesítése): Két halmaz (A és B) uniója azon elemek összessége, amelyek az vagy A-ban, vagy B-ben legalább az egyikben benne vannak.Jelölése:
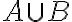
Metszetképzés (halmazok közös része): Két halmaz (A és B) metszete azon elemek összessége, amelyek A-ban és B-ben is benne vannak.
Jelölése:
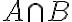
Különbségképzés: Két halmaz (A és B) különbsége azon elemek összessége, amelyek A-nak elemei, de B-nek nem.
Jelölése: A \ B
Részhalmaz: Az A halmaznak a B halmaz részhalmaza, ha B valamennyi eleme A-nak is eleme.
Jelölése:
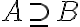 (vagy
(vagy 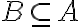 )
)
Valódi részhalmaz: Az A halmaznak a B halmaz valódi részhalmaza, ha B valamennyi eleme A-nak is eleme, de A-nak van legalább egy olyan eleme, amely nem eleme B-nek.
Jelölése:
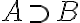 (vagy
(vagy 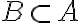 )
)
Ha ez nem teljesül, azaz B nem valódi részhalmaza A-nak, akkor azt így jelöljük:
Komplementerképzés: Egy adott A halmaz komplementerbe azok a H-beli elemek tartoznak bele, amelyek A-nak nem elemei, az H\A halmaz vagy alaphalmaz.
Jelölése:
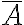
Üreshalmaz: az a halmaz, amelynek nincs eleme.
Jelölése:
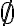
Direkt (Descartes) szorzat: A és B direkt szorzatának eredményeképpen olyan számpárokat kapunk, amelyeknek első tagja A-nak eleme, második tagja B-nek eleme.
Jelölés:
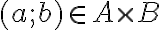 , ahol
, ahol 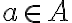 és
és 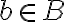
Halmazműveletek (nagyítva)
3. Tulajdonságok
Tetszőleges A halmazra érvényesek a következők: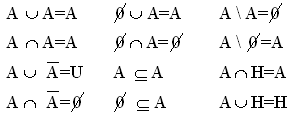
Fontos!!!
- A halmaz elemei mind különbözőek. (Nincs két azonos eleme.)
- Nincs az elemek között rendezettség, azaz nem képezünk sorrendet az elemek között.
Utolsó módosítás: 2014. augusztus 4., hétfő, 23:12